01ICLR 2026 (Oral)
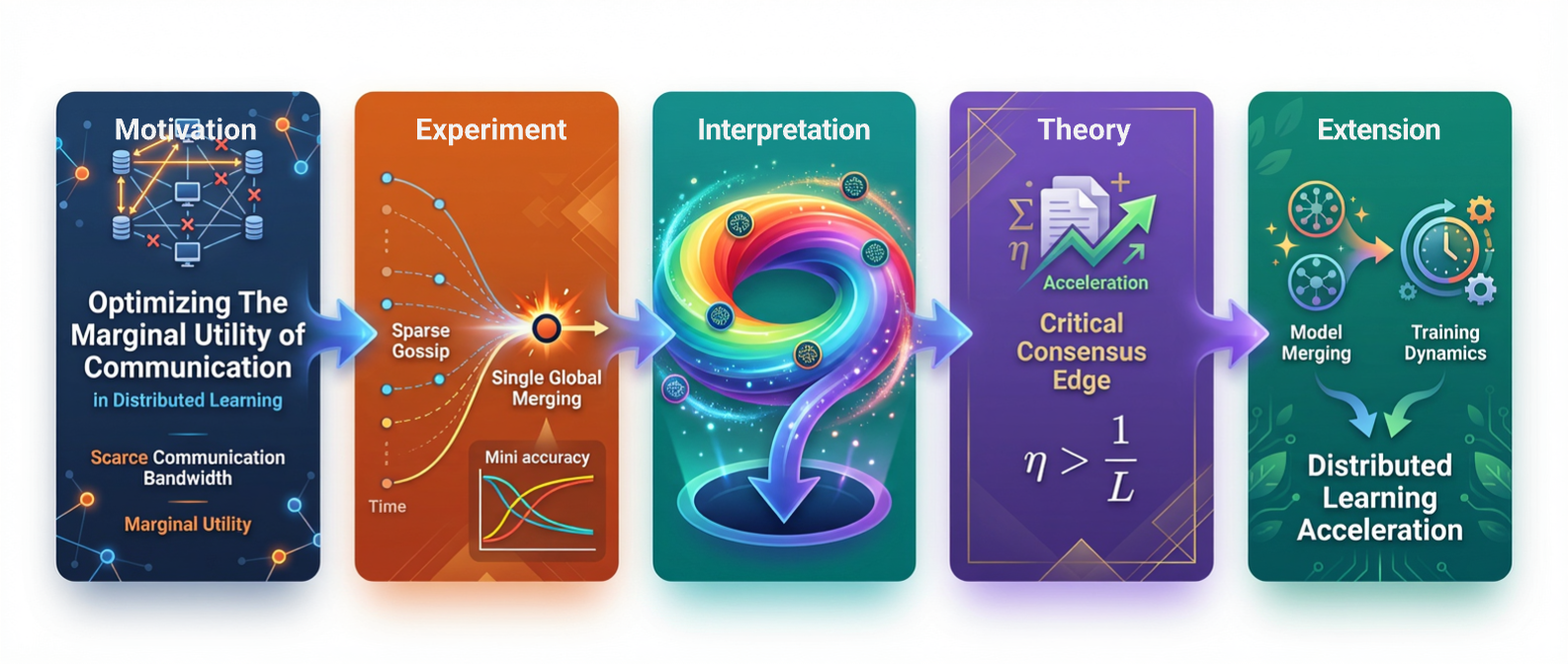On The Surprising Effectiveness of a Single Global Merging in Decentralized Learning
A single final merge can recover performance after sparse communication, connecting model mergeability with decentralized training dynamics.
Research archive
All publications
Research on learning mechanisms, decentralized training, and related problems. Google Scholar ↗
2026
02Preprint 2026
Distributed Team Orchestration via Supervisor Networks: Convergence, Optimality, and Resilience
Supervisor networks coordinate team learning under imperfect beliefs, with resilience to misleading reports from Byzantine teams.
03Springer 2026 (Book chapter)
Imagining a Democratic, Affordable Future of Foundation Models: A Decentralised Avenue
A review of decentralised foundation models, covering shared resources, incentive mechanisms, and training in heterogeneous environments.
2025
04ICLR 2025
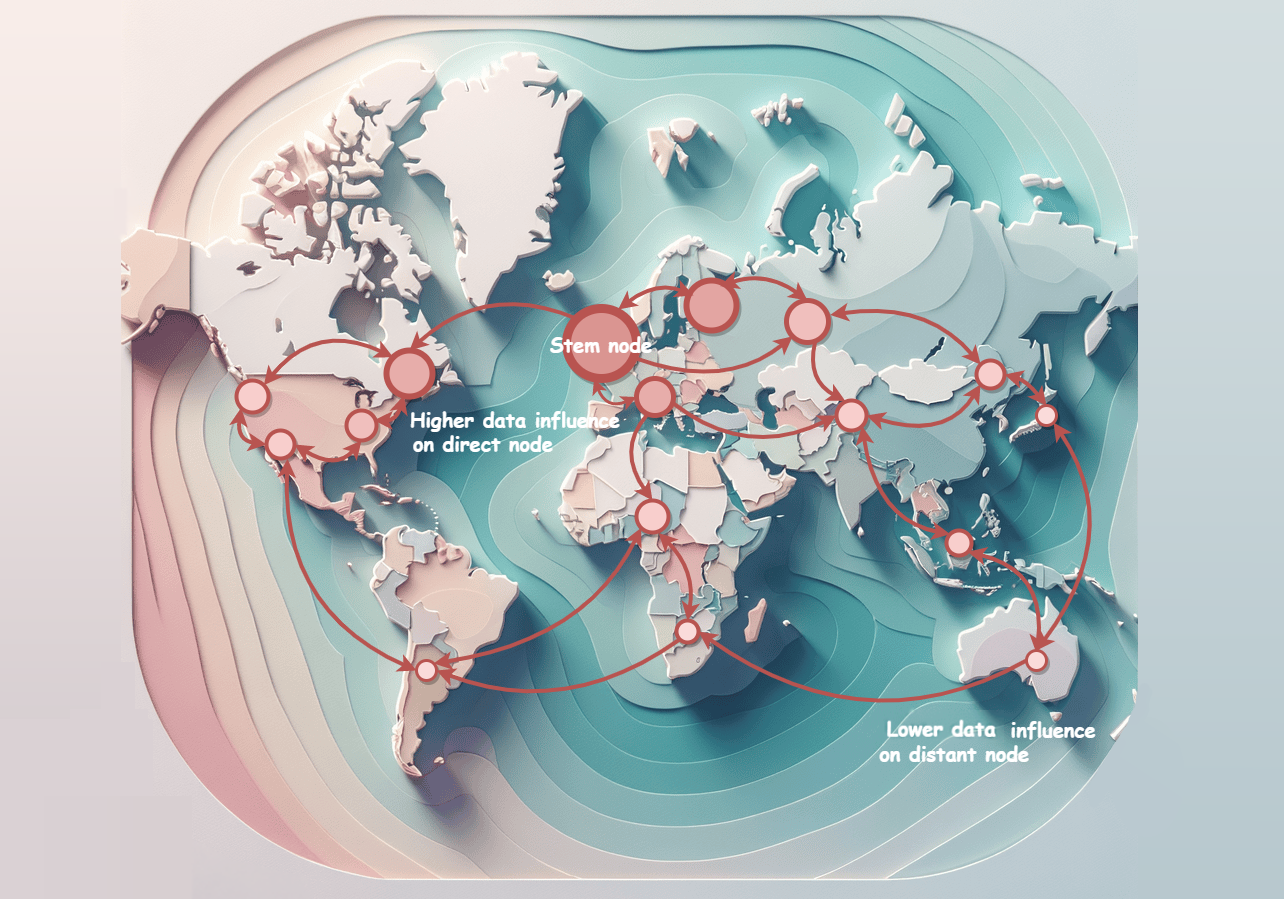DICE: Data Influence Cascade in Decentralized Learning
DICE traces how data influence cascades through a decentralized network, shaped by data, communication topology, and loss curvature.
05TMLR 2025
Lie Symmetry Net: Preserving Conservation Laws in Modelling Financial Market Dynamics via Differential Equations
Lie Symmetry Net incorporates symmetries and associated conservation laws when learning solutions to differential equations.
2023
06ICML 2023
Decentralized SGD and Average-direction SAM are Asymptotically Equivalent
Decentralized SGD and average-direction SAM are asymptotically equivalent, connecting decentralized training with implicit sharpness regularization.
07KDD 2023
Improving Expressivity of GNNs with Subgraph-Specific Factor Embedded Normalization
SuperNorm incorporates local subgraph structure into normalization to improve GNN expressivity and alleviate over-smoothing.
08ECAI 2023
Adversarial Erasing with Pruned Elements: Towards Better Graph Lottery Ticket
ACE-GLT reconsiders pruned graph connections and model weights to refine sparse graph lottery tickets.
09AAAI 2023 (Oral)
Contrastive Identity-Aware Learning for Multi-Agent Value Decomposition
Contrastive identity-aware learning distinguishes agents’ temporal credits to encourage diverse behaviors in cooperative multi-agent learning.
2022
10ICML 2022 (Spotlight)
Topology-aware Generalization of Decentralized SGD
Network topology affects how decentralized SGD generalizes, linking graph connectivity with learning performance.